|
Basic Introduction to
Ultra-cold Matter
We work with atomic gases at ultra-low
temperatures (10-1000 nK). At these extremely low temperatures, the physics of
the gas is no longer classical and can only be described by the laws of quantum
mechanics. When a system is made of identical indistinguishable particles,
quantum mechanics predicts that the particles will obey two mutually exclusive
sets of rules called quantum statistics. Particles with integer spin obey
Bose-Einstein statistics and are called bosons. Particles
with half-integer spin obey Fermi-Dirac statistics and are called
fermions. The effects of quantum statistics are only observable
typically at ultra-cold temperatures.
Bosons
All particles with integer spin, such as photons,
gluons, and some atoms, are bosons. Identical bosons tend to clump together in
the same quantum state. In the language of quantum mechanics, the total wave
function of identical bosons must be symetric under exchange of any of its
particles.
When bosons are cooled to ultra-low temperatures,
they all tend to congregate in the ground state, or lowest energy level, of the
system which they constitute. Bosons tend to do this even when the average
energy of the particles is several times the energy spacing between levels --
nevertheless, the system must be very cold. This ultra-cold clumping phenomena
is called Bose-Einstein condensation (BEC). When a system of particles
condenses to BEC, it is a very abrupt phenomena that happens at a specific
critical temperature, Tc. While the existence of a BEC was predicted by
Einstein in 1921, it was observed for the first time at JILA (Boulder,
Colorado, USA) in 1995 by Carl Wieman and Eric Cornell in a dilute gas of
bosonic rubidium atoms (rubidium-87).
One can see the transition to BEC by looking at images of the
atomic cloud. A sharp peak in the density appears at the BEC phase transition:
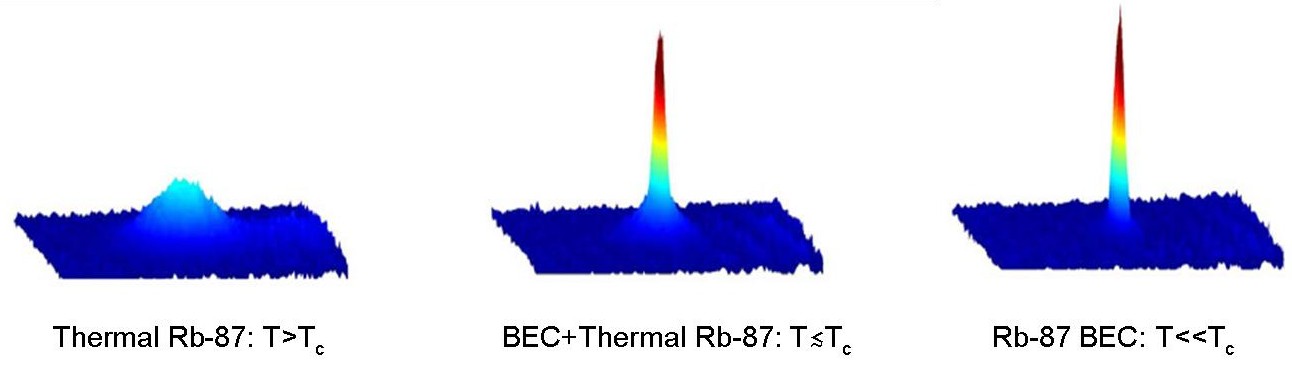
[Data for images courtesy of the Thywissent lab, University of
Toronto]
|
A BEC in atoms is similar to a laser with photons. In both cases
multiple bosons (aotms or photons) occupy a same quantum state.
Fermions
Particles with half-integer spin, such as
electrons, quarks, protons, neutrons, and some atoms (the ones that are not
bosons), are fermions. Identical fermions tend to avoid each other and obey the
Pauli exclusion principle: Identical fermions cannot occupy the same quantum
state. According to quantum mechanics, the total wave function of identical
fermions must be anti-symetric under exchange of any of its particles.
When fermions are cooled, the system loses energy,
but the particles cannot all occupy the lowest energy level due to the Pauli
exclusion principle. Instead, the paticles fill up the energy level ladder up
to an energy determined by the number of particles. This energy is called the
Fermi energy, EF, and also sets the
temperature (Fermi temperature, TF)
at which Fermi-degeneracy becomes appears. When the system is close to filling
up the energy ladder, the particles are said to form a degenerate Fermi gas
(DFG). The following cartoon illustrates the transition from a thermal gas to a
DFG:
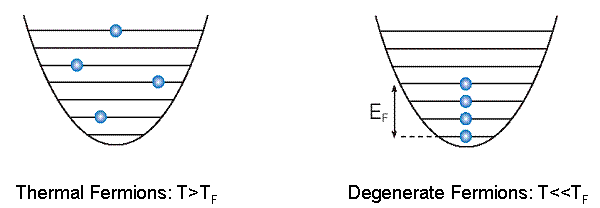
|
The transition from a thermal gas to a DFG is not
abrupt, but rather a smooth continuous process, and does not display any strong
qualitative feature such as the bimodal distribution of a BEC. On July 14,
2005, we observed a gas of Fermi-degenerate potassium-40 atoms for the first in
our lab, and the first ever to do so in a chip micro-magnetic trap. The
following images show a K-40 gas above and below the Fermi temperature -- the
red circle indicates the position of the Fermi energy, EF:
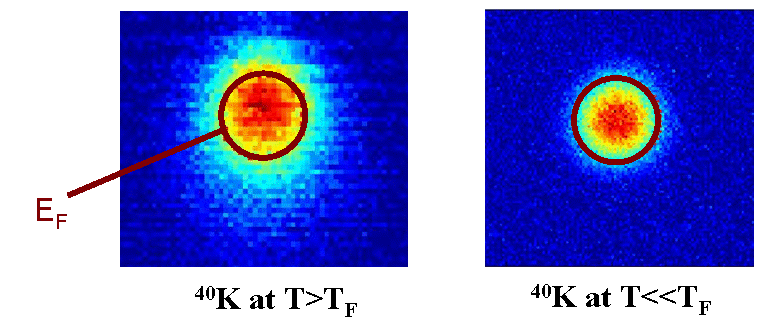
[Data for images courtesy of the Thywissen lab, University of
Toronto]
|
Once the K-40 atoms have been cooled to below the
Fermi temperature, further cooling does not significantly reduce the atomic
cloud size with respect to the "Fermi radius" associated with Fermi energy.
|
