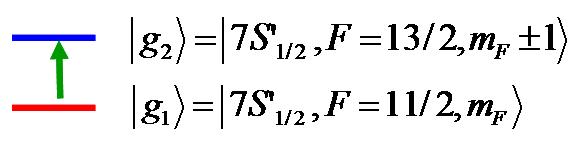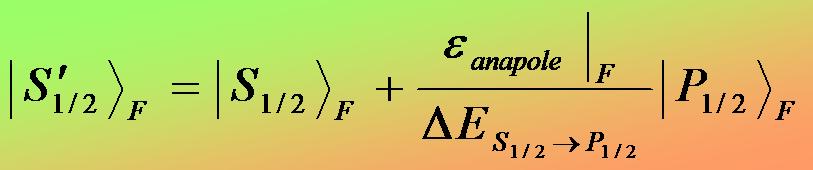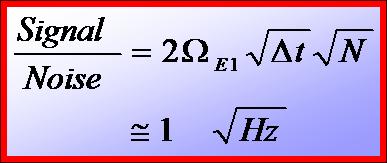Proposed nuclear anapole moment measurement

   The nuclear anapole moment of francium is an order of magnitude larger than in cesium, the only atom in which a non-zero moment has been measured [C. S. Wood et al., Science 275, 1759 (1997)]. We propose a measurement of the parity-violating nuclear anapole moment of francium in a string of isotopes using an microwave cavity to drive a forbidden hyperfine transition.

What's an anapole moment?

   An anapole moment is a rarely considered classical electromagnetic moment. The anapole is a localized moment, which manifests itself as a contact interaction . For a charged particles in an electromagnetic field, the interaction with the anapole of the field occurs only at a single point.
   A common example of an electromagnetic field with an anapole moment is the field generated by a toroidal current : since almost all of the electromagnetic energy is in the magnetic field inside the torus, an electron will primarily interact with such field when it is inside the torus. Part of that localized interaction can be described by an interaction with a point-like anapole moment located at the center of symmetry of the torus.
   The interaction of a charge with an anapole moment is in sharp contrast with the motion of a particle moving in an electromagnetic field with a dipole moment: In this case, the charged particle interacts with the dipole field at all points in space.

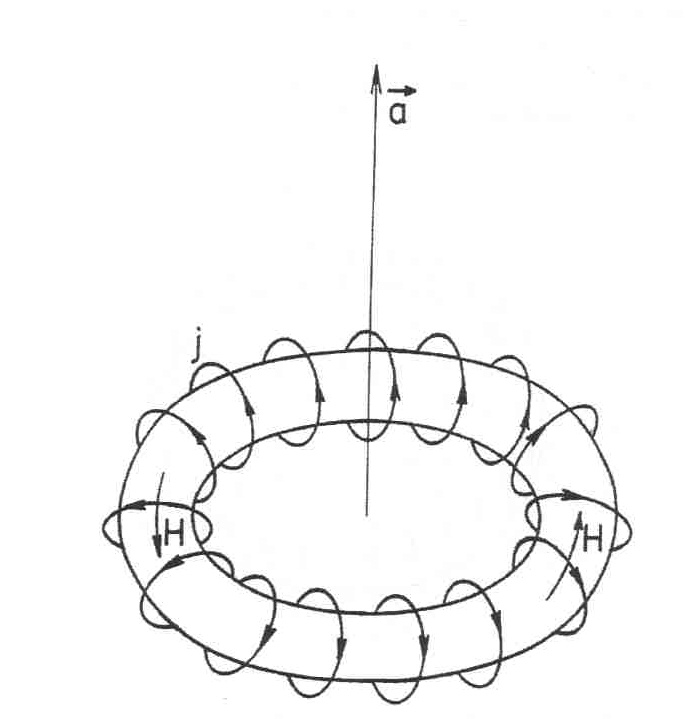
Example of a current distribution with an anapole moment: Toroidal current
[figure taken from V. V. Flambaum in Atomic Physics 16: Sixteenth International Conference on Atomic Physics.,edited by W. E. Baylis and G. W. F. Drake (AIP, 1998)].

The anapole moment

The anapole moment of an arbitrary current distribution, J(r), is: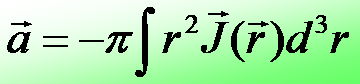

The vector potential generated by an anapole moment a at the origin is: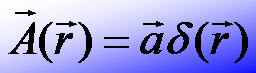

The interaction potential of an electron with an anapole moment a is: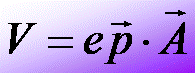

 Parity non-conservation

  The interaction energy between an electron and a classical anapole moment is even under a parity time-reversal transformations (in both transformations: p Y -p, J Y -J). However, a circulating current also implies angular momentum (L=r x p), which is even under a parity transformation (LY L), with the anapole moment parallel to the angular momentum (a // L) -- in quantum mechanics this is also necessary according to the Wigner-Eckart theorem. So from this second analysis, the interaction energy is odd under a parity transformation: the anapole interaction violates the parity even symmetry of the hamiltonian.

   In the nucleus, the spin and the circulating orbital motion of the external nucleons generate the nuclear spin I and an associated  effective current. However, the weak force introduces a small toroidal component to this orbital+spin current, thus generating a parity violating anapole moment. The small toroidal component is due to the exchange of the Z⁰ neutral weak current between nucleons, which is represented in the Feynman diagram below:

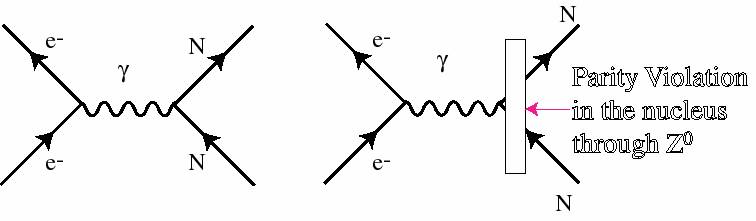
Feynman diagrams for the regular electron-nucleon interaction (left)
and the parity violating electron-anapole interaction (right)

Proposed measurement method

   We propose to measure the anapole moment of francium nuclei by searching for the induced parity non-conserving spin-dependent transition amplitude between two hyperfine ground levels.

Parity mixing:

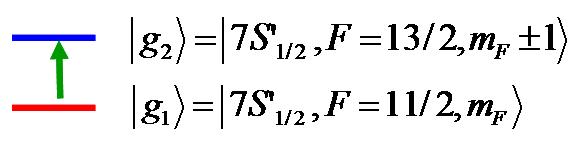
Parity forbidden E1 hyperfine transition

   Since the hamiltonian is no longer a purely parity-even operator due to the parity-odd anapole interaction, the energy eigenstates no longer have a definite parity. More specifically, an |S, state is now mostly even, but contains a little bit of an odd |P, state contribution. Expanding the new "|S'," state to 1st order in the parity conserving basis, we get

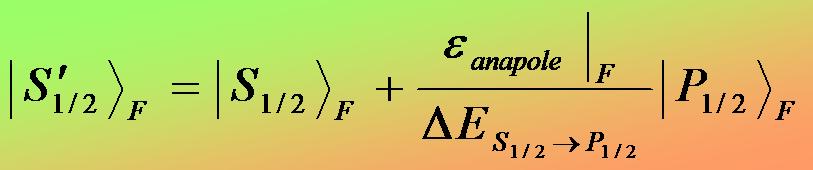
where DE is the energy separation of the 7S_1/2 and 7P_1/2 levels (~817 nm), and e_anapole is an energy characterizing the anapole induced parity mixing. This parity mixing  means that a parity forbidden E1 transition between hyperfine ground states is now possible.

Fundamental signal-to-noise

   While the amplitude for such a transition is very small, it is nevertheless observable. According to our calculations, such a transition amplitude is an order of magnitude larger in francium than in cesium. The proposed measurement is ultimately quantum projection noise limited. We estimate that the signal-to-noise will be

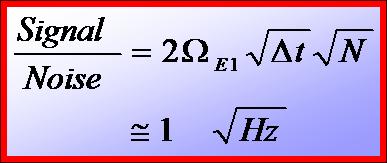
Where W _E1 is the Rabi-frequency of the anapole-allowed E1 transition. We have assumed a measurement on 10⁶ francium atoms in a microwave electric field of 1 kV/m. While the ultimate signal-to-noise may appear small, it is large compared to standard parity-violation measurements.

For more detailed information on the proposed measurement, please see
   S. Aubin, E. Gomez, J. M. Grossman, L. A. Orozco, M. R. Pearson, G. D. Sprouse, and D. P. DeMille
   Francium spectroscopy and a possible measurement of the nuclear anapole moment
   ICOLS XV proceedings , ed. S. Chu, V. Vuletic, A. J. Kerman, and C. Chin, World Scientific (2001). [PDF]

   E. Gomez, S. Aubin, G. D. Sprouse, L. A. Orozco, and D. P. DeMille
   Measurement method for the nuclear anapole moment of laser trapped alkali atoms
   arXiv:physics/0412124 -- submitted to Phys. Rev. A.

For a good review of the nuclear anapole moment, please see
   V. V. Flambaum in Atomic Physics 16: Sixteenth International Conference on Atomic Physics.,edited by W. E. Baylis and G. W. F. Drake (AIP, 1998).